Similarity transformation may refer to. Learn more about spotting similarity transformations with this tutorial.

8 G 1 Translations Rotations And Reflections Rally Coach Teacher Lessons Coordinate Grid Student Work
The scale factor of a similarity transformation is the product of the scale factors of the dilations in the composition.
. Sample Solution Describe the sequence of transformations that map n PQR to nSTU. To check whether two figures are similar you need to check two things. The matrix representation of a general linear transformation is transformed from one frame to another using a so-called similarity transformation.
Circle A and circle B both have center -2 -7. Matrix similarity for matrix transformations of the form A P 1 AP. Given a pair of figures in the coordinate plane determine whether they are similar based on whether it is possible to map one to the other using angle-preserving transformations.
This is the currently selected item. If you can find a similarity transformation that maps one figure to the other then the figures are similar. New York State Common Core Math Geometry Module 2 Lesson 12.
Circle A can be mapped to circle A by a translation. A matrix has been discussed as a linear operation on vectors. For example if is the matrix representation of a given linear transformation in.
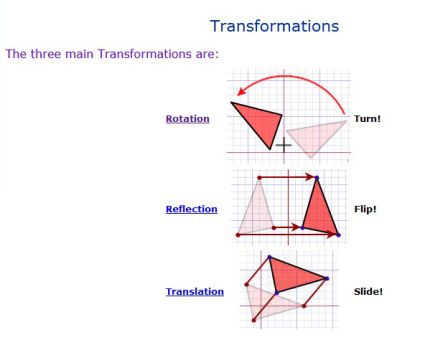
Rational equations intro. Two figures are similar if one can be obtained from the other by a sequence of translations reflections rotations and dilations. Two geometric fi gures are similar fi guresif and only if there is a similarity transformation that maps one of the fi gures onto the other.
Students define a similarity transformation as the composition of basic rigid motions and dilations. You will use a technology tool to move a shape on a coordinate graph using slides flips and turns and will use integers to describe those moves. A similarity transformation or similarity is a composition of a finite number of dilations or basic rigid motions.
Engage NYs files Mathematics High School. If you can find a similarity transformation that maps one figure to the other then the figures are similar. 7-2 Similarity and Transformations Lesson Quiz.
We examined a similarity transformation with scaling factor α 12 from one circle x 2 y 2 1 to another circle x 2 y 2 05 2 Figure 17aThe training step consisted of learning a set of complex-valued weights and thresholds such that the input set of straight line points indicated by solid circles in Figure 17a provided as output the half-scaled straight line points indicated. Similarity transformation definition a mapping of a set by which each element in the set is mapped into a positive constant multiple of itself the. X y x - 2 y - 11.
I can reason that a. Understanding the properties. In many applications the coordinate system or laboratoryframe of the vector that gets operated on is the sameas the vector gets returned.
Describe and perform transformations of. A similarity transformation takes one triangle and creates a similar triangle. Then circle A can be mapped to.
If playback doesnt begin shortly try restarting your device. The matrix itself is defined in terms of the coordinate systemof the vectors that it operates on--and that of the vectorsit returns. Students can describe a similarity transformation applied to an arbitrary figure ie not just triangles.
Similar triangles have congruent angles and. I can define similar figures as corresponding angles are congruent and corresponding side lengths are proportional. I can apply the concept of similarity to write similarity statements.
P0 21 is transformed to S0 22. Second you need to. This section will introduce similarity and congruence for polygons.
Prove that circle A with center 0 4 and radius 4 is similar to circle B with center -2 -7 and radius 6. A similarity transformationis a dilation or a composition of rigid motions and dilations. And is the representation of the same linear transformation in.
What Are Similarity Transformations and Why Do We Need Them. Use the graph to describe the changes in coordinates of the vertices of the triangles. Similar fi gures have.
If two figures are similar there must be a sequence of translations reflections rotations andor dilations that can transform one to the. First you need to check to see if all the corresponding angles are congruent. Describe the effect of dilations translations rotations and reflections on two-dimensional figures using coordinates.
If there are no dilations. Similar figures have the same shape but they may have different sizes. Students define two figures to be similar if there is a similarity transformation that takes one to the other.
Given a figure I can translate rotate reflect it. 210 Lesson 20 Transformations and Similarity urriculum ssociates opying is not permitted Transformations and Similarity. Similarity geometry for shape-preserving transformations.
Learn more about spotting similarity transformations with this tutorial. Similarity disambiguation Transformation disambiguation Affine transformation. I can recognize the symbol for similar.

Geometry Resources Transformations Math Teaching Geometry Gcse Math

Dilations And Similarity Worksheet Geometry Worksheets Math Worksheets Transformations Math

Transformations Practice Packet 8th Grade Math Reflection Math 8th Grade Math Transformations Math

Translations Rotations Reflections Glide Symmetries And Tesselations Reflection Math Transformations Math Math Rotations
0 Comments